physics – Saul Theory

October 10, 2018April 10, 2020

On the Gravitational Wave Detections

Hello everyone! Some people have asked me to post about my opinion on the recent claims that gravitational waves have been observed. There are a lot of things about these discoveries worth pointing out in such an informal arena as this one, so sure why not. I am partially adopting an earlier post on this topic, so my apologies for any disjoint trains of thought.

First off, lets begin by pointing out that these claims are sensational. Really amazing! To claim observation of something as exotic as merging black holes, using a new kind of exotic sensing device which has never detected anything before, is nothing short of sensational.

You may have surmised by now that I have been somewhat skeptical about these claims. This is really the only move available to a scientist. One has to be skeptical. This is called being a scientist. If you are religious or a fanatic, you will believe what people tell you based on their clothing, reputation, or credentials. There is a well known logical fallacy known as “appeal to authority”. If you are a scientist, you will question what they tell you and try to come up with your own experiments or models to verify or confirm what they told you. To a scientist, a Nobel prize awarded to some theory or another is a reason to pay attention to that theory – a good reputation is a reason to take a look. However it says nothing about the validity of the theory or observations. Those must come with understanding and experiment.

Big Science

This leads us to the general conundrum of what they call “big science”. This kind of science includes all experiments that are expensive or difficult enough that they can’t be repeated easily. For traditional science, repeating an experiment is the very heart of progress and the scientific method. However, for these “big science” experiments, we cannot so do. Does this mean we should reject all results from big science? Not at all. It just means that the science is a work in progress. It means we are waiting for the next round of experimenters to verify the results, and it means that we still have work to do. Good stuff!

Gravitational Waves – We all knew they are real

OK so on to the gravitational waves. The first thing that needs to be said is that gravitational waves are real. There is no denying this. Gravity is, no matter what formulation you prefer, capable of producing a force, or at least one that looks like a force to observers. This force is at least somewhat related to the direction of a source. Therefore, if we move the source – we have changed the force field. This change in force field will propagate outwards and we can call it a gravitational wave. For the electromagnetic force, this is what we call light – exactly that thing that happens when we accelerate a charge. All light of all frequencies is created by acceleration of charge in exactly this manner. Similarly, we know that moving an active gravitational source (like any mass) we will change the force field and produce a gravitational wave. At question here is not whether gravitational waves exist, we know they do. There is no way they couldn’t. What is at question is the details about how they can be measured with what apparatus, and how strong they are – and what objects have created them. Different types of General Relativistic theories might produces certain different magnitudes of waves for example, while a modified Newtonian theory might produce others. Different accelerated sources will also of course produce different signatures in gravitational radiation. What kind of acceleration of masses exists around us to observe is another question. The speed of propagation is another interesting question, and one that remains to some degree open. We won’t discuss it further here but interested readers are recommended to look at the excellent papers debates by Steve Carlip and Tom Van Flandern.

OK lets get on to some problems with the LIGO experiment and its ilk. The biggest problem in my mind is that the experiment is uncalbibrated. To somebody who has worked on scientific instruments, this is shocking. However, it may be unsurmountable. The problem basically is that the instrument has not looked at any control source. Consider for example Galileo’s first telescope. To see that it worked, he focused on a far off mountain or a ship. This enabled confidence in his new device, which only then did he point towards the heavens. To have trusted some device pointed at the heavens when nothing else had ever been viewed through it, well this is what we are told to do by the authors of the LIGO papers. Particle detectors are calibrated with known particle beams, just as voltmeters are calibrated with known voltages to assure that they are accurate. So, is it possible to calibrate these detectors with a local source?

Calibration attempt: drop a 100 kg mass onto the ground

Lets look at the gravitational radiation which this will create and compare it to the radiation from the source claimed by Abbott et al. Sure, a 100kg object is really massive, but we’re talking big science here.

First off there is the difference in mass. The 100 kg test mass is $6*10^{29}$ times smaller than the 30 solar mass black hole. That’s going to make a lot less radiation right? Well yeah. Especially because the radiated power is proportional to the square of the source. That’s a factor of $3.6*10^{59}$ .

How about the distance? Well a light year is $9.5*10^{12}$ km. 1.3 billion light years is therefore $1.3*10^{22}$ km. This supposed black hole merger event is $1.3*10^{25}$ times further away than our test mass dropping on the ground one meter away. Oh, and don’t forget that the intensity of the radiation falls off as the cube of the distance from dipole sources. (Edit: gravitational radiation is always quadrupolar so the field may fall off even faster. However some have argued that the power falls of as the square of the distance, and that this power is directly measured by the LIGO device, which if true would change the conclusions here). The intensity attenuation from our black hole merger due to distance from source will be a whopping $2.2*10^{75}$ times larger than the attenuation of radiation from our test mass.

The only thing missing from our back of the envelope calculation here is the acceleration applied to the mass. After all, it is acceleration of a source which causes radiation. A stationary charge does not light make, nor does a stationary mass emit gravitational waves. For the test mass, lets assume we are going from 10m/s to 0m/s in 0.001 seconds when the thing hits the ground (because it’s soft ground, the test mass is soft, and it takes some time to stop the test mass). That’s an acceleration of 10000 m/s/s or about 1000 Gs (commercial crash test accelerometers go to 2000Gs or higher).

For the black holes it isn’t too hard to put an estimate on the acceleration. The Schwarzchild radius of the black holes they report as about 210 km. This means when they touch, the centers of mass will be 420km apart. Using this one estimates using the Newtonian limit of about twenty billion m/sec/sec or 2 billion Gs:

$A=G*m_2/r^2 = 2.2*10^{10} m/sec^2$

Buckle your seatbelt!

It’s the square of the acceleration which determines the emitted power from an accelerated source, thus our difference between the falling test mass and the black hole will be a factor of $5.0*10^{12}$ .

–

That’s it! OK lets recap the three relevant differences between our emitting systems and see how we did:

–

A) Source magnitude squared- Black holes ~ $3.6*10^{59}$ times larger

–

B) Attenuation – Black holes ~ $2.2*10^{75}$ times smaller

–

C) Acceleration squared – Black holes ~ $5.0*10^{12}$ times larger

–

Add it up and what do you get? The gravitational radiation from the test mass hitting the ground could be about 1200 times stronger than the radiation from the distant alleged black hole merger.

Granted, this is a back of the envelope calculation. The proper calculation of acceleration and radiation will take into account relativistic effects and precise orbital mechanics. Stopping our massive test mass in a millisecond might not be possible. But these are second order effects and the point remains: terrestrial sources of gravitational radiation should be visible if such distant sources are also visible. Just imagine that you could drop much more massive object than 100kg, such as an asteroid. Accelerations could also be larger than the 1000 Gs estimate. A landslide might not be a great calibrated source but clearly would be a strong emitter. How about 100 cars all colliding with a reinforced concrete wall simultaneously? All in the name of science of course. 100 not enough? Let’s make it 1000 in the second round of proposals. CMEs might be a perfect test.

EDIT: the number one comment on this discussion is that in the far field we don’t really attenuate our radiation as fast as the cube of the distance. If we assume that our detector is capable of detecting a variation in g field with amplitude which decreases only as the square of the distance, then it appears we are still some 20 orders of magnitude shy of reaching a similar signal with our test mass! However this neglects the fact that most of the attenuation will occur before we reach the transition zone to the far field (“Fraunhofer region”), when our distance from the source becomes sufficiently far that we can ignore any internal dynamics. What happens here is that the power in the near field falls off as the 4th power of distance (see MWT “Gravitation” for an explanation of why gravitational radiation is all quadrupolar). If we take ~50 km as the wavelength of the radiation, then a rough estimate of this transition zone will be 100 km away from the source. This provides a factor of 10^5^-4 = 10^-20 in attenuation of signal before we reach the far-field zone! In other words, for the purposes of this estimate, we are very similar in our predication of amplitudes between our very nearby test mass and our extremely distant black hole merger. Note that an even more simple estimate of total radiated power, followed by an assumption of spherical symmetry, does not capture the real attenuation due to the multipole nature of the radiation. Our improved estimate leaves us with one order of magnitude lower signal from the test mass, in other words – we can multiply our test mass by 10 on increase the acceleration on it by 10 to match the signal of black hole mergers.

Coincident with Gamma Ray Burst

On Sept. 15, 2014, a LIGO signal was observed and coincident with this signal a gamma ray pulse was observed by the Fermi gamma ray telescope. (!!!) This was too close for coincidence, appearing 0.4 seconds later and the team calculated a 0.22% probability of such an event occurring randomly. If this were bright enough it would alone confirm that LIGO was seeing something important and real (despite the lack of calibration). Unfortunately the team from INTEGRAL gamma ray telescope put a damper on this sensational claim by putting a low upper limit on the gamma ray emission (they didn’t see a serious burst). Another team re-analyzing the Fermi data concluded that there wasn’t much of a burst there either. The jury is still out, for a review of the debate see https://arxiv.org/abs/1801.02305.

Conclusions

I am a huge fan of interferometry science and the LIGO and VIRGO projects. However we should be careful to jump to any conclusions at this stage of Big Science. I expect that future gravitational wave observations will have something to say about the early conclusions here, and I especially await any team that can observe the radiation from a more local source, an asteroid impact or a CME or even a laboratory source could fit the bill. Until then I would suggest more cautious language such as “we may have seen black holes merging”, or “signals consistent with black holes merging” as this exciting field isn’t to a high enough level to rule out other sources for the observed signals.

EDIT 2)

There seems to be some pushback on the signal processing methods used to pull out the signal in the alleged observations:

https://arxiv.org/abs/1711.07421

It could also be that other known sources (other than CMEs, impacts mentioned earlier) could be used for calibration:

https://www.space.com/white-dwarf-binary-gravitational-wave-source-discovery.html

October 22, 2017December 19, 2017

Bell’s Gambit Declined

Introduction

Hello Everyone.

Some of you may be aware of a mission I have recently joined: to help scientists clean up and add precision to the dialog concerning our chess game of understanding quantum mechanics.

In a recent essay (中文）I outlined a three pronged attack to better teach this topic and better understand the implications. One of these prongs concerns elimination of the terms “nonlocality” and “noncausality” which some authors have been pushing as necessarily implied by experiments and theory of quantum mechanics. The attack we can make with a tempo on this heavily popularized line is a deadly one, and I wrote up and published one version of it under the name “The Emperor Has No Nonlocality” in 2015 (preprint). Today I’m going to go over this game and explain for you how I recommend you play this position on the board.

To briefly review before we get started, “The Emperor Has No Nonlocality” outlines a potentially crushing move against those who wish to push the line that quantum mechanics is incompatible with local realism. We accomplish this by locating the heart of the problem, and demonstrating that it can be explained with local physics.

Well really, I didn’t locate this heart, David Mermin located it for us. Many professors and authors have pointed to Mermin’s immortal description of the EPR paradox as the most accessible one, and the most clear for students or those who might be unfamiliar with some of the notation used by other authors. In this article he even explicitly invites us to solve the puzzle using local physics, which is exactly the path we take, following the work of David Bohm and others. It is my hope that this solution of his gedankenexperiment will enable others to see this opening with a tempo to the heart of nonlocality, and enable us to proceed to tackle more formidable foes and to a much stronger understanding of the physics.

The Gambit Begins

But wait, you say: doesn’t everybody know that quantum mechanics is inconsistent with local physics? What about Bell’s theorem and the associated experimental work?

Indeed, this is where the game gets interesting. Bell’s immortal 1964 paper putting forth his gambit is in my opinion extremely well written. I’ve gone through it dozens of times over more than two decades. It is a miniature, to the point, and doesn’t indulge in the sometimes tempting academic pursuits of lengthening, obfuscation, and over-referencing. If I had to find another paper of this style I would be tempted to mention the Mathematical Theory of Communication by Claude Shannon, and if you know something about my preferences you will know this is the highest compliment I can find for an academic paper. To put it succinctly, Bell plays a sharp game. His game comes in first getting us to accept a set of notations and a definition, after which he leaves us struggling to deal with the consequences.

John Stewart Bell

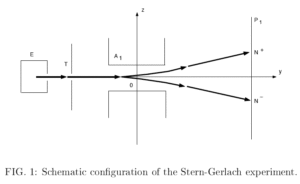
The gambit appears immediately in Bell’s equation one, in which he presents a “definition of local realism”, in the context of the Stern-Gerlach experiment:

$A = A(\vec a,\vec \lambda )$

$B=B(\vec b,\vec \lambda)$

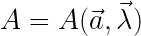
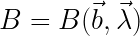
where

$A, B = \pm 1$

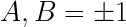
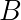Here we have the results of two measurements $A$ and $B$ , measurements of the deflection of two electrons which have passed through Stern-Gerlach devices and been registered on detectors.

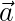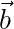These measurements, according to Bell’s gambit, depend only as calculable functions on the orientation of the relevant measurement apparatus ( $\vec a$ or $\vec b$ ) and the internal state of the electron prior to entering the device ( 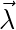$\vec\lambda$ ). The result of this measurement, we are told, can only be up or down (1 or -1), and Bell emphasizes that the measurement 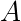$A$ cannot depend on the orientation of the 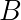$B$ apparatus ( 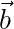$\vec b$ ), nor can the measurement 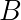$B$ depend on the orientation of the 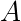$A$ apparatus ( $\vec a$ ).

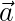It certainly is consistent with the use of the word “local” in that if these measurements did depend on the other settings far away, there would be nonlocal behavior at work.

Furthermore, Bell provides us with a means to arrive at a probabilistic distribution – by considering a set of many electron states each 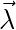$\vec \lambda$ , with some distribution 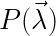$P(\vec\lambda)$ . This he handily provides in his equation 2. At this point he tells us already what fate is in store for us – that the probability arrived at by this formalism CANNOT be that predicted by the formalism of quantum mechanics!

At this point the reader is invited to pause the video and follow Bell’s argument, if the reader has not already done so, or if the general mathematical formalism is not appreciated the reader should then read the Mermin version of the EPR paradox which spells out the same line of Bell’s gambit in a specific example and therefore a more accessible and less symbolic manner. Or, for those of you who just want to enjoy the game, simply continue reading.

Bell’s Gambit Accepted

Jose Raul Capablanca tells us that the best way to refute a gambit is to accept it.

The traditional approach here is to accept Bell’s gambit, and allow reference to this basic assumption (Equation 1) as the assumption of “local realism”. Unfortunately this line of reasoning has led to what is usually a losing game (a poor or inconsistent understanding of the physics). One line follows the acceptance of the gambit with pursuit of ever-smaller “loopholes” which will enable experiments to remain in accord with Bell’s principle of local realism. Some experimentalists have become quite stubborn in their insistence that all such loopholes are closed , and if this is true than this line of counterattack is truly over. Others maintain some loopholes remain open. Some of the loopholes proposed certainly seem desperate, while others – not so much. Most notably the “detection efficiency loophole” or “fair sampling loophole” appears quite compelling, and we will see that our suggested line in this piece, Bell’s gambit declined, transposes into something which at least seems quite similar to the detection efficiency loophole. But you will see this later.

The only other line of counterattack following acceptance of Bell’s gambit is to pursue a line which is not dependent on any local realism. This desperation leads to a wide variety of chaotic lines, most of which I believe should simply be resigned. Some people suggest that superluminal signalling is possible (even though no evidence exists for superluminal communication, and signalling should enable communication), or that “multiple universes” might be required (on the microscopic level only?) to explain the behavior, and various other hand-waving. Perhaps even stranger is that some pursue the total denial of objective reality and the suggest that the mere conscious registering of a measurement somehow physically changes the world. At this point it appears we have taken a line of self delusion rather than admit that we have made a blunder.

The trouble is not that these ideas have no merit, it is that they contradict the very point of studying physics to begin with. In fact such “spooky” (a word used all too often in these discussions) lines of reasoning can be taken at the macroscopic level as well. There are many things which cannot be named. There are no shortages of mysteries and if this is your pursuit, I encourage you. I also enjoy such pursuit. However the general goal of a communicable physical theory is precisely to describe some subset of our observations of the world in a consistent and useful model. If our efforts in producing such a coherent model wind up with an incoherent model we need to call spooky, it’s time to admit that we have lost the match and try another strategy. Let’s not forget the object of the game now.

Perhaps we should step back and look at places where we may have blundered in our attempts to understand the physics and return again to the board after a short break.

Bell’s Gambit Declined

Usually pop science reporters are not scientists themselves, in that it is their job to report on what scientists have hypothesized and tested rather than to hypothesize and test things themselves. So you might be surprised then to see that Forbes reporter Chad Orzel hits the nail exactly on the head in his article on “quantum loopholes”:

Quantum particles […] are more strongly correlated than possible with any theory in which the measurement outcomes are determined in advance.

OK, so in much of the article he shows that he has been trapped into following the Bell’s Gambit Accepted line, but in this passage he correctly assesses the content of Bell’s so-called “principle of local realism”. The principle does not include all local realistic theories, but only those local realistic theories in which the outcome of a measurement is exactly determined in advance!

This gives us a line of attack which enables us to decline Bell’s gambit, as we know from basic measurement theory, information science, as well as chaos theory, that with a finite ( i.e. limited ) amount of information 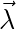$\vec \lambda$ it is impossible to predict the results of future measurements to arbitrary precision. Thus we could say that Bell’s principle of local realism isn’t realistic at all.

But that’s not all.

Bell’s gambit also allows for only two outcomes after the electron with state 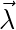$\vec\lambda$ enters the apparatus: either it orients itself aligned upwards to the field gradient and is deflected upward creating a detection event at the upper plate or it orients itself downwards to the field gradient and is deflected downward creating a detection event at the lower plate. This doesn’t allow for the electron to be deflected elsewhere upon entering the device, including internal absorption or reflection, nor does it allow for the electron to arrive at a dead zone on the detector to not register at all. After all, the detector is never going to have 100% efficiency and so the assumption that 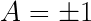$A=\pm1$ cannot be correct. This is where the Bell’s gambit declined line can transpose to look something like the detection efficiency loophole or David Bohm’s “local variable plus nondetection” model. This latter model indeed can explain the predicted (and observed) probabilities while still being a local and realistic theory.

A bifurcation diagram showing a chaotic system which can branch or quantize chaotically.

To summarize: we can deny that Bell’s equation 1 contains all local theories, because it clearly contains only those local theories which include deterministic binary measurement. This refutation opens up an entirely different line of play in our chess game of understanding quantum mechanics.

We can for example describe the result of the Stern-Gerlach experiment to be at first binary (the electron will go one way or the other), but then take the probability of detection to depend on the original angle of the electron spin. This is the simplest line to play following Bell’s gambit declined, as it enables a local theory consistent with predictions of QM with a minimum of added machinery. We can visualize the electron reorienting itself as it experiences torque in the inhomogenous magnetic field, and then losing some of it’s likelihood of detection (via internal state changes or some sort of deflection) in the process.

However other lines are also possible. The initial binary choice could involve external probabilities as well, and the detection probability could have other dependencies.

Variations after Bell’s Gambit Declined

There are some potential refutations to Bell’s Gambit Declined. One such refutation is to assert that the state 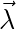$\vec \lambda$ in Bell’s description of local realism can contain not just the internal state of the electron but also every possible externality to arbitrary precision. If this is the case, then indeed the experimental result must be a function of this vector. There is no longer any room for probabilistic measurement if every possible external factor is now included. There is no longer any room to decline the gambit. However such a construction leaves much to be desired. Not only is the size of 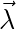$\vec \lambda$ now necessarily uncountably infinite, but the elements of it are also infinite. The assumption of a “calculable function” now no longer seems to hold. This is an interesting variation but one that appears to be more desperate for the player who is trying to refute Bell’s Gambit Declined. It doesn’t appear to be a comfortable position to play.

Another potential refutation could come from asking further details of the external factors that can affect the measurement and seeking to poke holes in the exact physical model which appears as the game progresses, and the players continue to refine their physical model of the system at hand (electron + inhomogeneous field + detector apparatus). In this case there will be many other battles over details, but at stake will not be whether the system could be classified as local or nonlocal, but over other details, for example of electron structure or the nature of the interaction with the inhomogeneous magnetic field.

Endgame?

So what then is an electron exactly, and what possible interactions take place as an electron moves through an inhomogeneous magnetic field? Well, good questions – and ones that you aren’t going to find all the answers for right here today.

Perhaps however you have found a way to open your exploration of these issues which doesn’t end in a quick checkmate or stalemate. There are plenty of ways that a model electron could behave, locally and realistically, to obey the laws of quantum mechanics. However there are no ways that it could pass through a Stern-Gerlach device such that our measurement is precisely determined in advance by finite internal or hidden variables in the electron. This is what we have really learned from Bell, Aspect, et al.

Thank you and see you all next time.

Acknowledgements

Agadmator’s chess channel.

Thanks to Agadmator for the vocabulary and format of this post 🙂